Disclaimer:
The authors are solely responsible for the content of this report. Material included herein does not represent the opinion of the European Community, and the European Community is not responsible for any use that might be made of it.
Back to overview reports
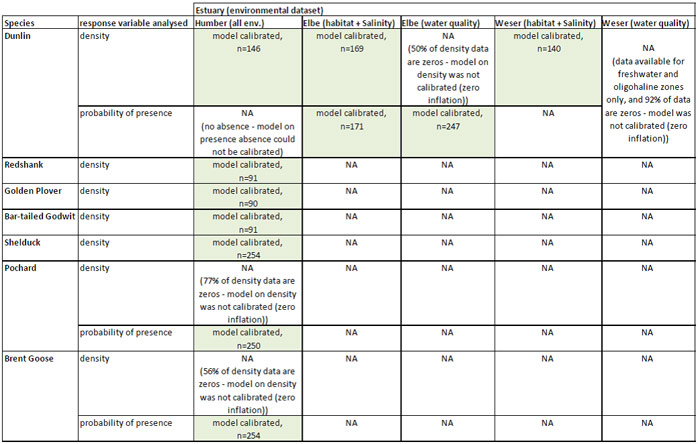
The species density by sector/counting unit by year was used as response variable. Only when the frequency of occurrence of the species in the dataset was <75% (mainly due to a more heterogeneous distribution of the species, with association to certain sectors/units and absence from others), the probability of presence was modelled as response variable (based on presence-absence data) by using a logistic regression. A summary of the models calibrated for the species in the three TIDE estuaries (including information on the size of datasets (n) analysed) is reported in the table below.
The environmental variables reported in Table 2 (in Chapter 4) were used as explanatory variables (covariates) and no interaction terms were considered between the predictors, in order to allow a simpler interpretation of model results. As for the multivariate analysis and due to data availability limitations (see also Appendices 1 and 3), separate models relating the species density distribution with either habitat areas or water quality variables were employed in the Weser and the Elbe, whereas the effects of all environmental variables were analysed simultaneously in a single model for the species in the Humber. However, salinity zone (Salz) was included as a factor in the analyses of habitat datasets in the Weser and Elbe in order to take account of the possible combined effect of habitat area and salinity gradient on the species distribution within these estuaries.
When necessary, data were transformed (square root, forth root or log transformation, whichever the most appropriate) in order to remove the possible effect of outliers, normalise the data distributions and to increase homogeneity of variance.
The number of candidate explanatory variables (or predictors) to be included in the model was firstly reduced by removing highly correlated variables. Following Fielding and Haworth (1995), a Spearman correlation analysis was conducted and variables with high correlation coefficient (|rS|>0.7) were not considered for model calibration, in order to avoid multicollinearity. In addition, given that even a moderate collinearity might be problematic, particularly if the ecological signal is weak (Zuur et al. 2009), variables with |rS|>0.6 were also considered and were excluded from the analysis whenever their relationship with the response variable was weak (|rS|<0.5).
Relationships between the species mean distribution and environmental variables were studied by means of generalized additive models (GAM) (Zuur et al. 2007). GAMs allow to model some predictors non-parametrically in addition to linear and polynomial terms (Guisan et al. 2002), allowing the decision of the response shapes to be fully determined by data. This is achieved by introducing a smoothing function for the continuous predictors. GAMs were fitted by using the ‘mgcv’ library (Wood 2000) for R software packages (R Development Core Team 2008). This type of model is represented in ‘mgcv’ as penalized GLM, each smooth term of a GAM being represented using an appropriate set of basic functions (Wood and Augustin 2002). The GAM model-building procedures followed the guidelines of Wood (2000), using penalized regression splines. This allows the degrees of freedom for each smooth term in the model to be chosen simultaneously as part of model fitting by minimizing the Generalized Cross Validation (GCV) score of the whole model (Wood, 2006). Density data were fitted using a Gaussian family with the canonical identity link, whereas presence–absence data were fitted using a binomial family with the canonical logit link, optimizing the GCV score. Model selection was carried out by means of backward selection using AIC as selection criterion. The resulting best model was validated graphically by examination of possible patterns in the residuals, in order to check that assumptions (homogeneity, independence, normality) were fulfilled. Single predictor models were also considered and their AIC value was used to rank the importance of each environmental variable in affecting the species distribution.
Back to top
What environmental factors should be considered in the design of a compensation scheme for waterbirds and their habitats?
What environmental variables are most important in determining minimizing or basic compensatory requirements for waterbirds?
What is important in establishing a zonation for estuaries?
What tools and guidance are available to minimise and mitigate disturbance to waterbirds?
Determinants of bird habitat use in TIDE estuaries
Table of content
- 1. SUMMARY
- 2. INTRODUCTION
- 3. STRUCTURE OF THE REPORT
- 4. DATA USED
- 5. GENERAL CHARACTERISTICS OF BIRD ASSEMBLAGES IN TIDE ESTUARIES
- 6. BIRD ASSEMBLAGES DISTRIBUTION AND RELATIONSHIP WITH ENVIRONMENTAL VARIABLES
- 6a. Humber
- 6b. Weser
- 6c. Elbe
- 7. SPECIES DISTRIBUTION MODELS
- 7a. Dunlin
- 7b. Redshank, Golden Plover and Bar-tailed Godwit
- 7c. Shelduck, Pochard and Brent Goose
- 8. DISCUSSION
- 9. CONCLUSIONS
- 9a. Analysis Conclusions
- 9b. Management Recommendations
- 9c. Recommendations for Future Studies
- 10. REFERENCES
- 11. APPENDIX 1
- 12. APPENDIX 2
- 13. APPENDIX 3
- 14. APPENDIX 4
14. Appendix 4
Details on the analysis on wader and wildfowl species distribution models in TIDE estuaries
Regression models were applied to single species (Dunlin, Golden Plover, Redshank, Bar-Tailed Godwit, Shelduck, Pochard and Brent-Goose) data and environmental variables within each estuary.The species density by sector/counting unit by year was used as response variable. Only when the frequency of occurrence of the species in the dataset was <75% (mainly due to a more heterogeneous distribution of the species, with association to certain sectors/units and absence from others), the probability of presence was modelled as response variable (based on presence-absence data) by using a logistic regression. A summary of the models calibrated for the species in the three TIDE estuaries (including information on the size of datasets (n) analysed) is reported in the table below.
The environmental variables reported in Table 2 (in Chapter 4) were used as explanatory variables (covariates) and no interaction terms were considered between the predictors, in order to allow a simpler interpretation of model results. As for the multivariate analysis and due to data availability limitations (see also Appendices 1 and 3), separate models relating the species density distribution with either habitat areas or water quality variables were employed in the Weser and the Elbe, whereas the effects of all environmental variables were analysed simultaneously in a single model for the species in the Humber. However, salinity zone (Salz) was included as a factor in the analyses of habitat datasets in the Weser and Elbe in order to take account of the possible combined effect of habitat area and salinity gradient on the species distribution within these estuaries.
When necessary, data were transformed (square root, forth root or log transformation, whichever the most appropriate) in order to remove the possible effect of outliers, normalise the data distributions and to increase homogeneity of variance.
The number of candidate explanatory variables (or predictors) to be included in the model was firstly reduced by removing highly correlated variables. Following Fielding and Haworth (1995), a Spearman correlation analysis was conducted and variables with high correlation coefficient (|rS|>0.7) were not considered for model calibration, in order to avoid multicollinearity. In addition, given that even a moderate collinearity might be problematic, particularly if the ecological signal is weak (Zuur et al. 2009), variables with |rS|>0.6 were also considered and were excluded from the analysis whenever their relationship with the response variable was weak (|rS|<0.5).
Relationships between the species mean distribution and environmental variables were studied by means of generalized additive models (GAM) (Zuur et al. 2007). GAMs allow to model some predictors non-parametrically in addition to linear and polynomial terms (Guisan et al. 2002), allowing the decision of the response shapes to be fully determined by data. This is achieved by introducing a smoothing function for the continuous predictors. GAMs were fitted by using the ‘mgcv’ library (Wood 2000) for R software packages (R Development Core Team 2008). This type of model is represented in ‘mgcv’ as penalized GLM, each smooth term of a GAM being represented using an appropriate set of basic functions (Wood and Augustin 2002). The GAM model-building procedures followed the guidelines of Wood (2000), using penalized regression splines. This allows the degrees of freedom for each smooth term in the model to be chosen simultaneously as part of model fitting by minimizing the Generalized Cross Validation (GCV) score of the whole model (Wood, 2006). Density data were fitted using a Gaussian family with the canonical identity link, whereas presence–absence data were fitted using a binomial family with the canonical logit link, optimizing the GCV score. Model selection was carried out by means of backward selection using AIC as selection criterion. The resulting best model was validated graphically by examination of possible patterns in the residuals, in order to check that assumptions (homogeneity, independence, normality) were fulfilled. Single predictor models were also considered and their AIC value was used to rank the importance of each environmental variable in affecting the species distribution.
Important to know
Reports / Measures / Tools
| Report: | Management measures analysis and comparison |
|---|
Management issues
How can management targets and monitoring strategies be set for waterbirds in compensatory areas?What environmental factors should be considered in the design of a compensation scheme for waterbirds and their habitats?
What environmental variables are most important in determining minimizing or basic compensatory requirements for waterbirds?
What is important in establishing a zonation for estuaries?
What tools and guidance are available to minimise and mitigate disturbance to waterbirds?